
Le système binaire est le système de numération utilisant la base 2.
On nomme couramment bit (de l’anglais binary digit, soit « chiffre binaire ») les chiffres de la numération binaire. Un bit peut prendre deux valeurs, notées par convention 0 et 1.
Dans ce type de codage, chaque nombre est représenté de façon unique par une suite ordonnée de chiffres. Et chaque position m représente une puissance (m − 1) de la base. Si l’on se limite dans un premier temps aux nombres entiers positifs, en base dix ces puissances sont : un (1), dix (représenté par 10), cent (dix fois dix, représenté par 100), mille (dix fois cent, représenté par 1000), dix mille, etc.
En base deux, ces puissances sont : un (1), deux (représenté lui aussi par 10), quatre (deux fois deux, représenté par 100), huit (deux fois quatre, représenté par 1000), seize (deux fois huit, représenté par 10000), etc.
Un nombre qui s’exprime en base B par les quatre chiffres 1101 s’analyse :
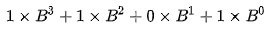
qui donne :
| 1101 en base B = 10 : | |||||
| 1101 en base B = 2 : |
Ou encore le nombre binaire 10100101
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
= 1×1 + 0x2 + 1×4 + 0x8 + 0x16 + 1×32 + 0x64 + 1×128 = 165

